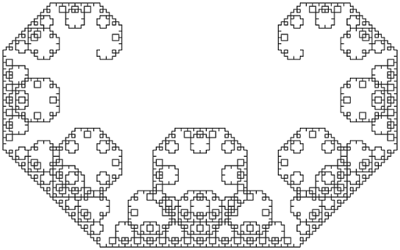
The Lévy C curve in... C

I've been reading about HTML and other web standards lately, and it eventually led me to SVG, a vector image format I've been meaning to look into for some time. By a fortunate coincidence, I had been reading about PostScript just prior to this, and SVG came naturally after that. So I set out to make my first SVG drawing, and after a while I decided on the Lévy C curve.

This:

Preparation: SVG

Let's get right to it. We're gonna make it using the SVG <path> element. The <path> element is made like this:

<!-- draws an equilateral triangle -->
<path d="M 0 0 L 100 0 L 50 86 Z"></path>

That is, the drawing commands are put in the d attribute. They are more or less similar to their PostScript cousins. The commands consist of an identifying letter followed by a pair of coordinates. Uppercase letters indicate absolute coordinates, whereas lowercase letters indicate relative (to the current point) coordinates. M stands for "moveto," and L "lineto." We won't need it in our C curve construction, but Z closes the current path, joining the current point to the first point.

The C curve

That's it for SVG. Now a little bit about the C curve itself. We start with a straight line:

Think of this line as being directed from A to B. In the next step, instead of going directly to B, we take a detour to point C:

Standing at A, and facing B, we turn right 45° and move 1/√2 times the distance AB to the point C. There, we turn left 45°, twice, and head for B. After reaching B, we turn right 45° once more, so we end up heading the same way we started.

To recap, we were standing at A, and facing B. Earlier, when we headed straight to B, we had an instruction:

F

That means, go forward. Later, we replaced F with

+F--F+

That means, turn right, go forward, turn left twice, go forward, and finally turn right (all turns are 45°).

Now, apply this substitution:

F → +F--F+

again to get:

++F--F+--+F--F++

which looks like this:

The new points have been marked D and E. To show one more iteration explicitly, the instruction for drawing the next step is:

+++F--F+--+F--F++--++F--F+--+F--F+++

which looks like this, where I haven't marked the new points:

Do this ad infinitum, and you've got yourself the Lévy C curve!

Doing the thing in C

Now, if you've been reading this far, you might be thinking to yourself, "Where is the (other) C that the title mentioned?" Well, I'm glad you asked, because that's what we're gonna do now. We're gonna write a program in C to do this drawing for us.

The crux of the program is a simple recursive function that takes the current recursion level, and a displacement in the form of two coordinates x and y:

void ccurve(int level, double x, double y) {
  // code goes here
}

The function checks if the recursion level is zero. If it is, there is nothing to be done, and it just draws the line and returns:

void ccurve(int level, double x, double y) {
  if (level < 1) {
    printf("    l %.2lf %.2lf\n", x, y);
  } else {
    // do something here
  }
}

The coordinates are written with two digits of precision because I didn't find much point in any more precision. The spaces at the beginning may look weird, but they are there so that the end result looks nicely indented. You probably wanna look at the SVG output, and not the SVG code itself, but we're not barbarians and we like to keep things aligned pretty. ;-)

Now, the interesting thing happens when the recursion level is not zero. That means, there's more work to be done. In particular, we calculate the detour point $\left(x_m,y_m\right)$ , and draw the two segments recursively. I won't show it here, but it's easy to see that the detour point is $\left(\frac{x-y}{2},\frac{x+y}{2}\right)$ . If that makes you frown, because it looks like we're turning left 45°, not turning right, then it's because we are. SVG considers the y-axis pointing down, so insofar as we're turning towards the positive y-axis, we are turning left. I know. Weird.

Don't forget to decrease the level by one when you make the recursive calls:

void ccurve(int level, double x, double y) {
  if (level < 1) {
    printf("    l %.2lf %.2lf\n", x, y);
  } else {
    double xm = (x-y)/2, ym = (x+y)/2;
    ccurve(level-1, xm, ym);
    ccurve(level-1, x-xm, y-ym);
  }
}

And... that's it! Remember to move to the initial point to get the whole thing started, and we're all done!

That's it for today, I think. Thanks a ton for reading, and I hope I'll see you around!

Show code

#include <stdio.h>
#include <stdlib.h>

void ccurve(int level, double x, double y) {
  if (level < 1) {
    printf("    l %.2lf %.2lf\n", x, y);
  } else {
    double xm = (x-y)/2, ym = (x+y)/2;
    ccurve(level-1, xm, ym);
    ccurve(level-1, x-xm, y-ym);
  }
}

void html_prolog() {
  printf("<!DOCTYPE html>\n");
  printf("<html>\n");
  printf("<body>\n");
}

void html_epilog() {
  printf("</body>\n");
  printf("</html>\n");
}

int main(int argc, char* argv[]) {
  if (argc < 2) {
    printf("Usage: ccurve level\n");
    return 0;
  }
  int level = atoi(argv[1]);
  // start
  html_prolog();
  printf("<div style=\"margin:auto;width:600px\">\n");
  printf("<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" height=\"600\" width=\"600\" stroke=\"black\" stroke-width=\"2\" fill=\"none\">\n");
  // start path
  printf("  <path d=\"\n");
  // move to starting point
  printf("    M 150 187.5\n");
  // draw curve
  ccurve(level, 300, 0);
  // end path
  printf("  \" />\n");
  // finish
  printf("</svg>\n");
  printf("</div>\n");
  html_epilog();
}